SECTION III.

Of the motion of bodies in eccentric conic sections.

PROPOSITION XI. PROBLEM VI.

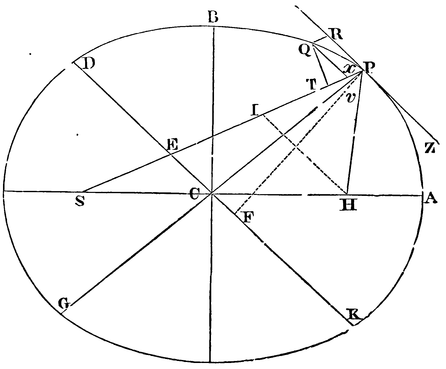
If a body revolves in an ellipsis; it is required to find the law of the centripetal force tending to the focus of the ellipsis.

Let S be the focus of the ellipsis. Draw SP cutting the diameter DK of the ellipsis in E, and the ordinate Qv in x; and complete the parallelogram QxPR. It is evident that EP is equal to the greater semi-axis AC: for drawing HI from the other focus H of the ellipsis parallel to EC, because CS, CH are equal, ES, EI will be also equal; so that EP is the half sum of PS, PI, that is (because of the parallels HI, PR, and the equal angles IPR, HPZ), of PS, PH, which taken together are equal to the whole axis 2AC. Draw QT perpendicular to SP, and putting L for the principal latus rectum of the ellipsis (or for $\scriptstyle {\frac {2BC^{2}}{AC}}$ ), we shall have L $\scriptstyle \times$ QR to L $\scriptstyle \times$ Pv as QR to Pv, that is, as PE or AC to PC; and L $\scriptstyle \times$ Pv to GvP as L to Gv; and GvP to Qv² as PC² to CD²; and by (Corol. 2, Lem. VII) the points Q and P coinciding, Qv² is to Qx² in the ratio of equality; and Qx² or Qv² is to QT² as EP² to PF², that is, as CA² to PF², or (by Lem. XII) as CD² to CB². And compounding all those ratios together, we shall have L $\scriptstyle \times$ QR to QT² as AC $\scriptstyle \times$ L $\scriptstyle \times$ PC² $\scriptstyle \times$ CD², or 2CB² $\scriptstyle \times$ PC² $\scriptstyle \times$ CD² to PC $\scriptstyle \times$ Gv $\scriptstyle \times$ CD² $\scriptstyle \times$ CB², or as 2PC to Gv. But the points Q and P coinciding, 2PC and Gv are equal. And therefore the quantities L $\scriptstyle \times$ QR and QT², proportional to these, will be also equal. Let those equals be drawn into $\scriptstyle \frac{SP^{2}}{QR}$ , and L $\scriptstyle \times$ SP² will become equal to $\scriptstyle \frac{SP^{2}\times QT^{2}}{QR}$ . And therefore (by Corol. 1 and 5, Prop. VI) the centripetal force is reciprocally as L $\scriptstyle \times$ SP², that is, reciprocally in the duplicate ratio of the distance SP. Q.E.I.

Lemma VII.

Pl. 2. Fig. 1.

The same things being supposed, I say that the ultimate ratio of the arc, chord, and tangent, any one to any other, is the ratio of equality. Pl. 2. Fig. 1.

For while the point B approaches the point A, consider always AB and AD as produc'd to the remote point b and d; and parallel to the secant BD draw bd; and let the arc Acb be always similar to the arc ACB. Then, supposing the points A and B to coincide, the angle dAb will vanish, by the preceding lemma; and therefore the right lines Ab, Ad (which are always finite), and the intermediate arc Acb, will coincide, and become equal among themselves. Wherefore, the right lines AB, AD, and the intermediate arc ACB (which are always proportional to the former) will vanish; and ultimately acquire the ratio of equality. Q.E.D.

COR 1. Whence if through B we draw BF parallel to the tangent, always cutting any right line AF passing through A in F, this line BF will ultimately be in the ratio of equality with the evanescent arc ACB; because compleating the parallelogram AFBD, it is always in a ratio of equality with AD.

COR 2. If through B and A more right lines are drawn, as BE, BD, AF, AG, cutting the tangent AD and its parallel BF; the ultimate ratio of all abscissas AD, AE, BF, BG and of the chord and arc AB, any one to any other, will be the ratio of equality. Cor. 3. And therefore in all our reasoning about ultimate ratio's, we may freely use any one of those lines for any other.

LEMMA XII.

All parallelograms circumscribed about any conjugate diameters of a given ellipsis or hyperbola are equal among themselves. This is demonstrated by the writers on the conic sections.

Proposition VI. Theorem V.

In a space void of resisŧance, if a body revolves in any orbit about an immoveable centre, and in the least time describes any arc just then nascent; and the versed sine of that arc is suppofed to be drawn, bisecting the chord, and produced passing through the centre of force: the centripetal force in the middle of the arc, will be as the versed sine directly and the square of the time inversely.

For the versed sine in a given time is as the force (by cor. 4. prop. 1.) and augmenting the time in any ratio, because the arc will be augmented in the same ratio, the versed sine will be augmented in the duplicate of that ratio, (by cor. 2 and 3. lem. 2.) and therefore is as the force and the square of the time. Subduct on both sides the duplicate ratio of the time, and the force will be as the versed line directly and the square of the time inversely. Q. E. D.

And the same thing may also be easily demonstrated by corol. 4. lem. 10.

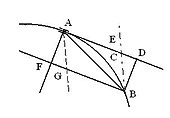
Cor. 1. If a body P revolving about the centre S, (Pl. 3. Fig. 2.) describes a curve line APQ which a right line ZPR touches in any point P; and from any other point Q of the curve. QR is drawn parallel to the distance SP, meeting the tangent in R; and QT is drawn perpendicular to the distance SP: the centripetal force will be reciprocally as the solid $\textstyle {\frac {SP^{2}\times QT^{2}}{QR}}$ , if the solid be taken of that magnitude which it ultimately acquires when the points P and Q coincide. For QR is equal to the versed sine of double the arc QP, whose middle is P: and double the triangle SQP, or SP x QT is proportional to the time, in which that double arc is described; and therefore may be used for the exponent of the time.

Cor. 2. By a like reasoning, the centripetal force is reciprocally as the solid $\textstyle {\frac {ST^{2}\times QP^{2}}{QR}}$ if ST is a perpendicular from the centre of force on PR the tangent of the orbit. For the rectangles ST x QP and SP x QT are equal.

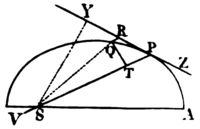
Cor. 3. If the orbit is either a circle, or touches or cuts a circle concentrically, that is contains with a circle the least angle of contact or section, having the same curvature and the same radius of curvature at the point P; and if P, V be a chord of this circle, drawn from the body through the centre of force; the centripetal force will be reciprocally as the solid $\scriptstyle ST^{2}\times PV$ . For PV is $\textstyle {\frac {QP^{2}}{QR}}$ Cor. 4. The same things being supposed the centripetal force is as the square of the velocity directly. and that chord inversely. For the velocity is reciprocally as the perpendicular ST; by cor. 1. prop. 1.

Cor. 5. Hence if any curvilinear figure APQ is given; and therein a point S is also given to which a centripetal force is perpetually directed; that law of centripetal force may be found, by which the body P will be continually drawn back from a rectlinear course, and being detained in the perimeter of that figure. will describe the same by a perpetual revolution. That is, we are to find by computation, either the solid $\textstyle {\frac {SP^{2}\times QT^{2}}{QR}}$ . of the solid $\scriptstyle ST^{2}\times PV$ , reciprocally proportional to this force.

Proposition I. Theorem I.

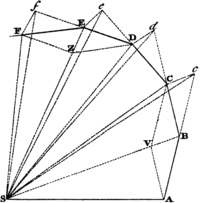
The areas, which revolving bodies describe by radii drawn to an immoveable centre of force, do lie in the same immovable planes, and are proportional to the times in which they are described. Pl. 2. Fig. 5.

OR suppose the time to be divided into equal parts, and in the first part of that time, let the body by its innate force describe the right line AB. In the second part of that time, the same would, (by law 1.) if not hinder'd, proceed directly to c, along the line Bc equal to AB; so that by the radii AS, BS, cS drawn to the centre, the equal areas ASB, BSc, would be described. But when the body is arrived at B, suppose that a centripetal force act at once with a great impulse, and turning aside the body from the right line Bc, compells it afterwards to continue its motion along the right line BC. Draw cC parallel to BS meeting BC in C; and at the end of the second part of the time, the body (by Cor. 1. of the laws) will be found in C, in the same plane with the triangle ASB. Joyn SC, and, because SB and Cc are parallel, the triangle SBC will be equal to the triangle SBc, and therefore also to the triangle SAB. By the like argument, if the centripetal force acts successively in C, D, E, &c. and makes the body in each single particle of time, to describe the right lines CD, DE, EF, &c. they will all lye in the same plane; and the triangle SCD will be equal to the triangle SBC, and SDE to SCD, and SEP to SDE. And therefore in equal times, equal areas are describ'd in one immovable plane: and, by composition, any sums SADS, SAFS, of those areas, are one to the other, as the times in which they are describ'd. Now let the number of those triangles be augmented, and their breadth dimnished in infinitum; and (by cor. 4. lem. 5.) their ultimate perimeter ADF will be a curve line: and therefore the centripetal force, by which the body is perpetually drawn back from the tangent of this curve, will act continually; and any describ'd areas SADS, SAFS, which are always proportional to the times of description, will, in this case also, be proportional to those times. Q. E. D.

Cor. 1. The velocity of a body attracted towards an immovable centre, in spaces void of resistance, is reciprocally as the perpendicular let fall from that centre on the right line that touches the orbit. For the velocities in those places A, B, C, D, E are as the bases AB, BC, CD, DE, EF, of equal triangles; and these bases are reciprocally as the perpendiculars let fall upon them.

Cor. 2. If the chords AB, BC of two arcs, successively described in equal times, by the same body, in spaces void of resistance, are compleated into a parallelogram ABCB and the diagonal BV of this parallelogram, in the position which it ultimately acquires when those arcs are diminished in infinitum, is produced both ways, it will pass through the centre of force.

Cor. 3. If the chords AB, BC, and DE, EF, of arcs describ'd in equal times, in spaces void of resistance, are compleated into the parallelograms ABCD, DEFZ; the forces in B and E are one to the other in the ultimate ratio of the diagonals BV, EZ, when those arcs are diminished in infinitum. For the motions B; and EF of the body (by cor. 1. of the laws) are compounded of the motions Bc, BV and Ef, EZ: but BV and EZ, which are equal to Cc and Ff in the demonstration of this proposition, were generated by the impulses of the centripetal force in B and E, and are therefore proportional to those impulses.

Cor. 4. The forces by which bodies, in spaces void of resistance, are drawn back from rectilinear motions, and turned into curvilinear orbits, are one to another as the vers'd sines of arcs described in equal times; which versed sines tend to the centre of force, and bisect the chords when those arcs are diminished to infinity. For such vers'd sines are the halfs of the diagonals mentioned in cor. 3.

Cor. 5. And therefore those forces are to the force of gravity, as the said vers'd sines to the vers'd sines perpendicular to the horizon of those parabolic arcs which projectiles describe in the same time.

Cor. 6. And the same things do all hold good (by cor. 5. of the laws) when the planes in which the bodies are mov'd, together with the centres of force which are placed in those planes, are not at rest but move uniformly forward in right lines.